본 글은 혁펜하임님 강의(https://www.youtube.com/watch?v=XsP3DGHwYf0)를 기반으로 정리 및 재구성한 글입니다.
1. 시스템과 LTI 시스템
시스템은 입력을 받아서 출력으로 내보내기 위해 형태를 바꿔주는 곳을 말한다. 넓게 지칭하면, 입력, 출력, 그리고 그 함수까지도 지칭하지만, 본 포스팅에서는 함수만을 의미하도록 한다. 즉, 다음 그림처럼 나타낼 수 있다.

위와 같이, 시스템은 입력을 출력으로 만들어주는 것들을 통칭하므로 매우 넓은 범위를 포함하며, 그 시스템이 갖는 성질에 따라서 특징을 정리할 수 있다. 이 중, Linearity (선형성)와 Time-invariant (시불변성)을 갖는 시스템을 LTI 시스템이라고 한다. 이 두 가지 특성은 시스템을 예측 가능 (Predictable)하게 해준다는 장점이 있으므로, 매우 중요하다. 각각에 대해서 살펴보도록 한다.
2. 선형 시스템 (Linear system)
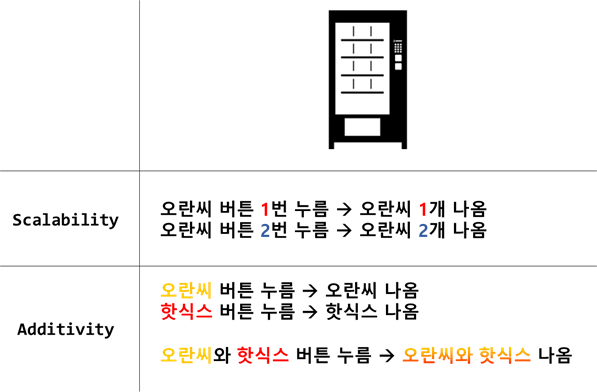
선형성 (Linearity)은 시스템뿐만 아니라, 여러 전공에서도 언급되는데 간단히 말해 Scalability (Scaling)과 Additivity를 일컫는 말이다. 이 두 가지 특성을 합쳐 Superposition이라고도 한다.
2-1. Scaling
입력이 x[n], 출력이 y[n]인 시스템에서 Scalable한 시스템은 다음을 만족한다.

이것을 수식으로 표현하면 다음과 같다.

2-2. Additivity
입력 x1[n]과 x2[n]에 대해 출력이 y1[n], y2[n]인 시스템에서 Additivity를 갖는 시스템은 입력 x3[n]=x1[n]+x2[n]에 대해 출력이 다음을 만족한다.
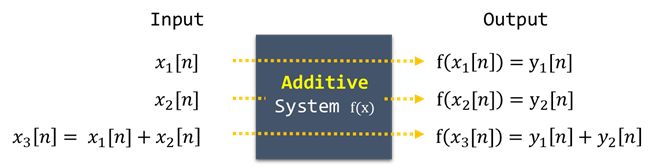
이것을 수식으로 나타내면 다음과 같다.
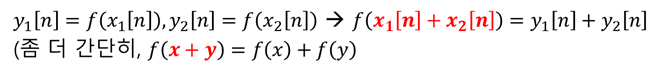
3. 시불변 시스템 (Time-invariant system)
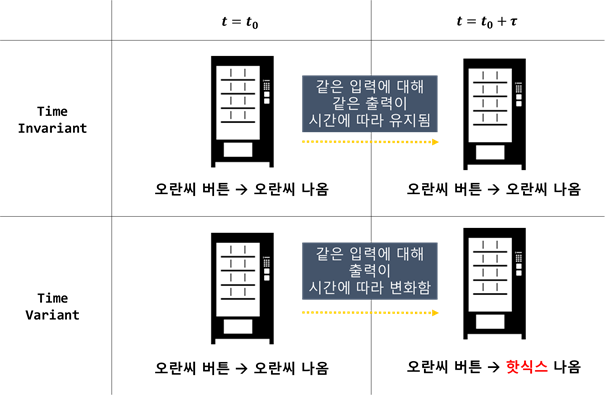
시불변이라는 것은 그 시스템에 대해서 input이 time-shift되었을 때도, output도 동일한 크기만큼 time-shift 된다는 것을 말한다.
자판기를 예를 들어 설명하면,
이것을 수식으로 나타내면 다음과 같다.
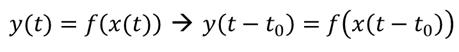
4. LTI 시스템을 고려하는 이유
LTI 시스템은 앞서 말한대로 예측가능한 시스템이라는 장점이 있다. ‘예측가능하다’라는 말의 의미를 되짚어보자면, 선형성으로 인해 입력이 2배 증가하면 2배의 출력이 생기고, 서로 다른 입력을 더했을 때는 선형적으로 더해진다는 것을 의미한다.
즉, LTI 시스템은 입력값을 다양하게 변화함에 따라 어떻게 출력이 나올지 예측할 수 있다는 것이다.
시스템을 만드는 인간의 입장에서 예측 가능한 시스템을 만들고, 그것을 기반으로 분석하는 건 큰 장점이다. 대부분의 물리현상은 비선형시스템이지만, 이렇게 예측가능한 LTI 시스템으로 근사시킴으로써 분석, 설계할 수 있다.
다음 포스팅에서는 LTI의 성질을 이용하여 컨볼루션의 개념에 대해서 정리한다.
